What to know about pricelists?
This is a great source > https://www.odoo.com/forum/help-1/the-almost-complete-guide-to-pricelist-behavior-185877.
Good practice to be able to raise prices in bulk by percentage
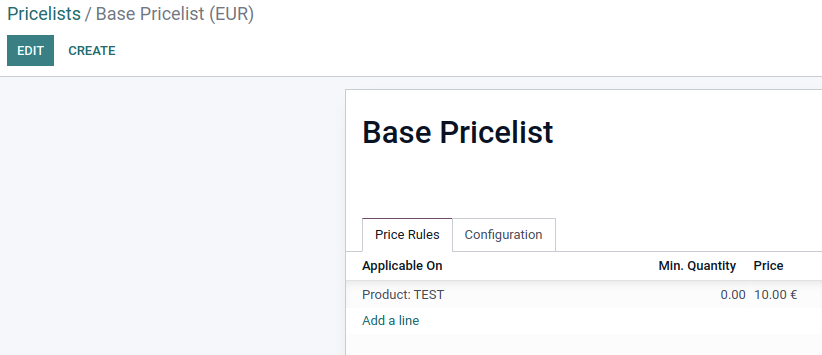
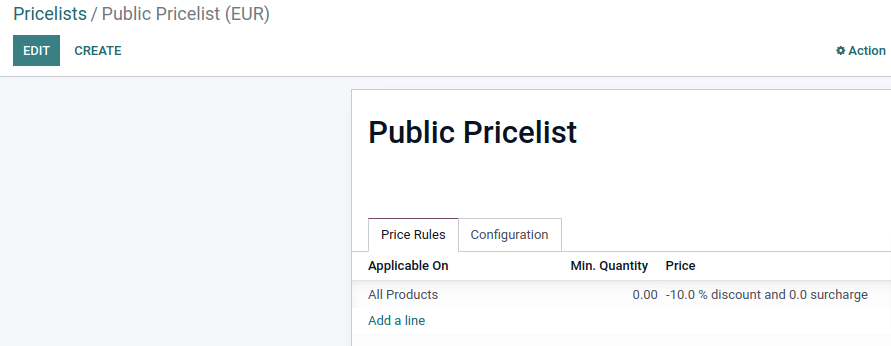
Add the prices of your products to a newly created Base Pricelist and derive the Public Pricelist (and/or others) from this pricelist adding the percentage. (You need to enable the 'Advanced price rules (discounts, formulas)' setting for this.)
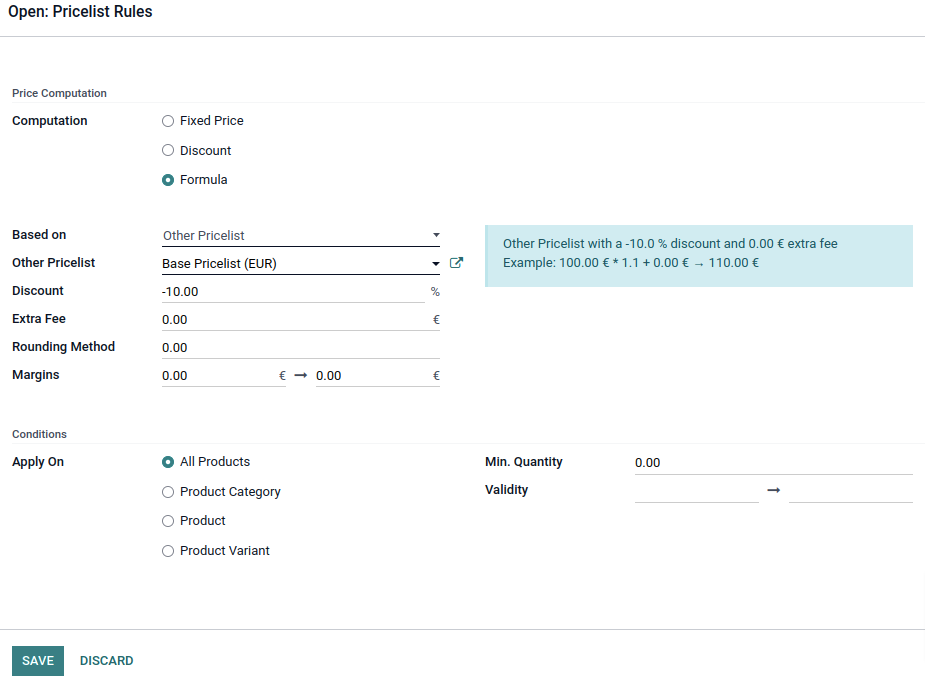
How does the rounding method work?
tools.float_round(discounted_price, precision_rounding=item.price_round)
def float_round(value, precision_digits=None, precision_rounding=None, rounding_method='HALF-UP'):
"""Return ``value`` rounded to ``precision_digits`` decimal digits,
minimizing IEEE-754 floating point representation errors, and applying
the tie-breaking rule selected with ``rounding_method``, by default
HALF-UP (away from zero).
Precision must be given by ``precision_digits`` or ``precision_rounding``,
not both!
:param float value: the value to round
:param int precision_digits: number of fractional digits to round to.
:param float precision_rounding: decimal number representing the minimum
non-zero value at the desired precision (for example, 0.01 for a
2-digit precision).
:param rounding_method: the rounding method used: 'HALF-UP', 'UP' or 'DOWN',
the first one rounding up to the closest number with the rule that
number>=0.5 is rounded up to 1, the second always rounding up and the
latest one always rounding down.
:return: rounded float
"""
rounding_factor = _float_check_precision(precision_digits=precision_digits,
precision_rounding=precision_rounding)
if rounding_factor == 0 or value == 0:
return 0.0
# NORMALIZE - ROUND - DENORMALIZE
# In order to easily support rounding to arbitrary 'steps' (e.g. coin values),
# we normalize the value before rounding it as an integer, and de-normalize
# after rounding: e.g. float_round(1.3, precision_rounding=.5) == 1.5
# Due to IEE754 float/double representation limits, the approximation of the
# real value may be slightly below the tie limit, resulting in an error of
# 1 unit in the last place (ulp) after rounding.
# For example 2.675 == 2.6749999999999998.
# To correct this, we add a very small epsilon value, scaled to the
# the order of magnitude of the value, to tip the tie-break in the right
# direction.
# Credit: discussion with OpenERP community members on bug 882036
normalized_value = value / rounding_factor # normalize
sign = math.copysign(1.0, normalized_value)
epsilon_magnitude = math.log(abs(normalized_value), 2)
epsilon = 2**(epsilon_magnitude-52)
# TIE-BREAKING: UP/DOWN (for ceiling[resp. flooring] operations)
# When rounding the value up[resp. down], we instead subtract[resp. add] the epsilon value
# as the approximation of the real value may be slightly *above* the
# tie limit, this would result in incorrectly rounding up[resp. down] to the next number
# The math.ceil[resp. math.floor] operation is applied on the absolute value in order to
# round "away from zero" and not "towards infinity", then the sign is
# restored.
if rounding_method == 'UP':
normalized_value -= sign*epsilon
rounded_value = math.ceil(abs(normalized_value)) * sign
elif rounding_method == 'DOWN':
normalized_value += sign*epsilon
rounded_value = math.floor(abs(normalized_value)) * sign
# TIE-BREAKING: HALF-UP (for normal rounding)
# We want to apply HALF-UP tie-breaking rules, i.e. 0.5 rounds away from 0.
else:
normalized_value += math.copysign(epsilon, normalized_value)
rounded_value = round(normalized_value) # round to integer
result = rounded_value * rounding_factor # de-normalize
return result